薄柔截面指的是宽厚比较大的构件。通过改变构件的截面形式来达到轻型钢框架的效果,既有良好的经济效益,又符合建筑行业发展“十三五”规划要求,目前已广泛应用于工业厂房以及低多层民用建筑。由于以薄柔钢框架建造的房屋满足绿色建筑结构体系要求,目前对薄柔型钢的研究主要集中在强度、刚度、稳定性能、冲击性能及内嵌或者外挂混凝土墙板等方面,对薄柔H型截面钢框架整体的抗震性能研究较少。相关文献通过对空间薄柔构件钢框架进行试验研究,发现薄柔截面构件的延性大小与截面宽厚比以及柱轴压比有较大关系,厚实截面相比薄柔截面更能发挥其延性能力。相关文献通过对薄柔截面钢框架进行承载力试验研究后发现薄柔H型截面钢构件有低延性的特点, 按 GB50011—2010《建筑抗震设计规范》设计时应按多遇烈度地震下的弹性计算。相关文献中考虑局部屈曲对于薄柔截面构件的影响,分析了悬臂梁的翼缘屈服长度、腹板高厚比和宽厚比之间的关系。相关文献通过试验和有限元方法对双向受弯且受压的非厚实I形梁的局部屈曲进行分析。相关文献通过对三维薄柔钢框架体系的极限强度试验,提出了“非弹性力矩再分配”效应。相关文献通过试验对薄柔H型钢的抗冲击性能进行了研究。相关文献在外挂再生混凝土墙板薄柔钢框架拟静力试验的基础上对高跨比等参数运用有限元软件进行滞回曲线研究,但未进行强弱轴、梁柱截面宽厚比、轴压比参数的研究。

本文基于已有的薄柔H型截面钢框架拟静力试验研究成果,在滞回曲线、骨架曲线及变形等方面进行模型有效验证;再通过轴压比、高跨比、截面宽厚比、强弱轴等不同的结构参数来探讨其结构抗震性能的影响,为薄柔截面H型钢框架结构体系的应用提供参考。

对一榀大比例尺的单跨双层强轴平面内的薄柔钢框架结构进行拟静力试验(图1)。其中柱与梁都选用热轧H型钢,材质为Q235B,梁柱节点为刚性连接,柱底与地梁用螺栓进行连接,地梁通过锚栓与地槽中的固定螺栓相连接,试件尺寸见表 1。

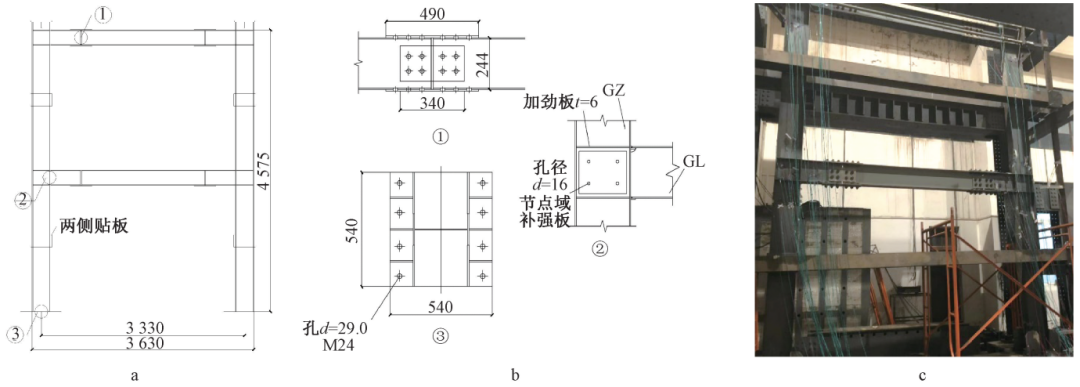
a—试件平面尺寸; b—详图尺寸; c—试验现场。 

图 1 单跨双层强轴平面内的薄柔钢框架结构 mm

表 1 试件尺寸   mm

试验采用行程±150 mm的电液伺服作动器在二层梁柱节点位置处对结构施加水平荷载。根据《土木工程结构试验》,选用混合幅值位移加载制度对结构控制加载,加载装置以及加载制度见图2。

a—加载装置; b—加载制度。

图 2 加载装置及加载制度

2.1 钢材本构关系

钢材本构采用双线性随动强化模型,采用von Mises屈服准则以及相关联的流动准则。有限元分析所采用的钢材材性参数均通过材性试验获得,具体结果见表2。

表 2 钢材的力学性能

2.2 有限元模型建立

本文采用ABAQUS程序,以试验实际尺寸建立有限元模型,按照试验加载制度进行有限元分析,将得到的骨架曲线与试验结果进行对比,分析验证模型的有效性。

有限元模型中所有部件均采用C3D8R实体单元。划分网格前需将部件切割,对各节点进行精细化网格划分,见图3a。试件梁柱节点、耳板均设置Tie连接;薄柔钢框架与地梁之间黏结良好,忽略其相对滑移,设置为全约束,并约束钢梁平面外 Z 方向位移(图3b)。在二层梁柱节点位置处进行位移加载,为防止应力集中,在加载端以及柱顶(验证模型时柱顶集中力为0)位置处设置耦合点(图3c)。

a—模型网格划分; b—模型边界条件; c—荷载耦合点。

图 3 有限元模型

3.1 滞回曲线与骨架曲线

有限元分析得到的滞回曲线和骨架曲线如图4所示。从图4a中可以看出,在位移加载初期,试验与有限元模拟的滞回环包络面积都很小,试件处于弹性阶段,结构刚度较大;当加载位移不断加大,试件达到屈服,开始耗能,滞回环不断往外扩张,环体逐渐饱满,有限元与试验的滞回曲线基本吻合较好,能反映承载力和刚度变化趋势,但有限元滞回曲线更为饱满,捏缩不明显;最终均出现承载力下降的阶段。

分析原因: 1) 试验时加载后期薄柔钢框架梁端开裂,连接件水平滑移量较大,导致其承载力下降; 2) 有限元分析时,未考虑钢梁与钢柱之间的滑移,导致有限元分析耗能高于试验结构(滞回环包围面积大于试验曲线); 3) 有限元分析时,材料的本构属性为理想状态,连接件的连接也是理想状态(连接件之间出现较大相对滑移)、螺栓与连接件之间无缝隙,所以有限元的捏缩现象且不明显,结构刚度有一定程度的增加。

有限元与试验的骨架曲线对比如图4b所示,可见:有限元骨架曲线与试验曲线吻合良好,但有限元初始刚度略大于试验值。原因如下:有限元分析时,忽略了试验模型存在的初始缺陷。

a—滞回曲线; b—骨架曲线。

图 4 滞回曲线和骨架曲线

有限元模拟和试验的骨架曲线特征点的相应值见表3所列,可见误差值在10%以内,且有限元模拟的承载力和刚度比试验的偏大。总体来看,有限元模拟骨架曲线和试验曲线吻合度较高,表明有限元计算可以较好地拟合结构的力学行为。结合图4b分析可以发现: 1) 试验以及有限元模拟都经历了弹性、弹塑性以及破坏阶段。2) 相比有限元模拟,试验得到的骨架曲线对称性稍差,这是因为试件在往复荷载作用过程中,地梁、螺栓连接位置处都会有轻微的不同程度滑移。

表 3 主要结果对比

3.2 应力、应变分析

试验过程中,在试件关键部位处粘贴应变片以观测试件在屈服前应变变化,应变片粘贴位置见图5。有限元仿真模拟试件达到屈服状态见图6,此时位移为 38.4 mm。可以看到:在柱脚外侧翼缘、梁端翼缘以及梁柱节点处应力达到 279~304 MPa,与试验测得关键部位应变值换算结果相吻合。

图 5 应变片布置

图 6 模拟试件达到屈服 MPa

当试件达到峰值荷载时,右侧柱脚发生屈曲(图7a),有限元模拟此位移加载下的柱脚位置处也发生了严重变形(图7b)。

a—试验柱脚屈曲; b—有限元柱脚屈曲。

图 7 柱脚屈曲

综合滞回曲线、骨架曲线以及应力、应变的分析可知:有限元模拟与试验有较好的吻合度。

为研究薄柔截面钢框架在不同参数下的抗震性能,以文中得到的有限元模型为对照组(BASE),通过改变其钢柱轴压比、高跨比以及柱梁的宽厚比进行分析。

通过对结构进行有限元模拟后得到其整体的滞回曲线,再从中提取骨架曲线后,可得到模型的关键数据,见表4。 

表 4 有限元分析结果

4.1 钢柱轴压比

只改变模型钢柱轴压比进有限元模拟分析,BASE为钢柱未加轴压力的模型,AC1~AC4分别为钢柱轴压比 n 为0.1、0.2、0.3、0.4的模型。通过有限元模拟计算得到的骨架曲线见图8。

图 8 不同钢柱轴压比模型的骨架曲线对比

分析可知:当轴压比从0.1增至0.2时,结构峰值位移下降了20%,峰值荷载下降了2.8%,初始刚度下降了0.4%;当轴压比从0.2增至0.3时,结构峰值位移下降了14%,峰值荷载下降了2.7%,初始刚度下降了 0.8%;当轴压比从0.3增至0.4时,结构峰值位移下降了16%,峰值荷载下降了2.2%,初始刚度下降了1%。由此可见,当钢柱轴压比增大时,结构的初始刚度、承载能力以及变形能力都在下降。 

4.2 高跨比

只改变模型高跨比进行仿真模拟,其中HS1和HS2只改变结构的层高,框架的跨度不变,HS1和HS2的高跨比分别为0.83,0.5,HS3只减小结构的跨度,不改变层高,高跨比为0.83,BASE的高跨比为0.66。模拟得到的骨架曲线见图9。

图 9 不同高跨比模型的骨架曲线对比

分析可知:当跨度不变、高度增加,高跨比从0.66增至0.83时,结构承载力下降了17%,初始刚度降低了37%,峰值位移提高了33%;反之,当跨度不变时,高跨比从0.66下降至0.5时,结构承载力提高了33%,初始刚度提高了58%,峰值位移降低了33%;当层高不变,跨度减小,高跨比从0.66增至0.83时,结构承载力提高了33%,初始刚度提高了8%,峰值位移提高了10%。由此可见:增大或减小结构的高跨比,对于结构的承载力、变形能力以及初始刚度都有一定的影响,在合理范围内选择结构高跨比,能够较好地改善结构的抗震性能。

4.3 构件宽厚比

只改变结构构件的宽厚比进行模拟分析,模型WT1以及WT2只改变腹板的宽厚比,翼缘宽厚比保持不变;模型WT3、WT4只改变翼缘宽厚比,腹板宽厚比保持不变。模型具体参数见表5。构件宽厚比对骨架曲线的影响见图10。

表 5 模型参数

图 10 不同构件宽厚比模型的骨架曲线对比

由结果分析可知:当增大腹板、翼缘宽厚比时,模型承载能力以及初始刚度都有了显著提升;当减小腹板、翼缘宽厚比时,模型承载能力以及初始刚度都有不同程度的降低;不过增大或减小构件宽厚比对峰值位移的影响较小,当腹板厚度从4.5 mm减小至3.5 mm时,结构承载力降低了16%,当翼缘厚度从6 mm减小至5 mm时, 结构承载力下降了7%;当腹板厚度从4.5 mm增加至5.5 mm时,结构承载力上升了11%, 当翼缘厚度从6 mm增加至7 mm时,结构承载力上升了3%。 

4.4 柱的强、弱轴方向

只改变框架柱的强、弱轴方向进行模拟分析,其他参数保持不变,BASE模型为框架柱在强轴平面内的框架,CO1模型为框架柱在弱轴平面内的框架。图11为两组模型骨架曲线的对比。

从数值模拟结果中可以发现:模型CO1在抵抗水平荷载时,由于柱子处于弱轴,其抵抗弯矩的能力变弱,柱比梁先屈服,造成了“梁强柱弱”的情况,不利于结构抗震。相比BASE模型,其承载力降低了40%左右,初始刚度降低了65%左右。在工程项目中,应当考虑结构实际工况,截面方向选择强轴为宜。

图 11 不同强、弱轴模型的骨架曲线对比