导读 排水系统的实时控制、不确定性分析、优化设计等常需要多次运行模型,并且模型结果要具有足够的精确性,因而计算速度和精确性都是评价模型适用性的关键指标。简化模型可以显著减少运算时间,但是会降低精确性。确定合适的简化模型结构,并优化参数率定方式有助于平衡上述两个指标,本文将提出一种可半自动完成上述工作的模型工具。
导读
排水系统的实时控制、不确定性分析、优化设计等常需要多次运行模型,并且模型结果要具有足够的精确性,因而计算速度和精确性都是评价模型适用性的关键指标。简化模型可以显著减少运算时间,但是会降低精确性。确定合适的简化模型结构,并优化参数率定方式有助于平衡上述两个指标,本文将提出一种可半自动完成上述工作的模型工具。
文章简介
作者利用水箱模型来表征排水系统,该模型涉及入流、出流和溢流,并遵循连续性方程。率定该模型需要的流量数据由Infoworks模型提供。该模型对系统的简化主要体现在对出流-储水量关系的假定上。
出流-储水量关系是简化模型的核心,注意到由于回水效应的存在,上升阶段的储水量要大于下行阶段的储水量。为能模拟这一现象,该文采用静态(Static Storage, Sstat)和动态储水空间(Dynamic Storage, Sdyn)结合的办法。Sstat用线性关系描述出流和蓄水量的关系,而Sdyn则假设与入流相关。当溢流发生时,由于存在显著的回水效应,Sdyn和入流之间的关系不再一一对应,为此引入额外静态出水空间,其与溢流相关。图1展示了出流和蓄水量间的关系。
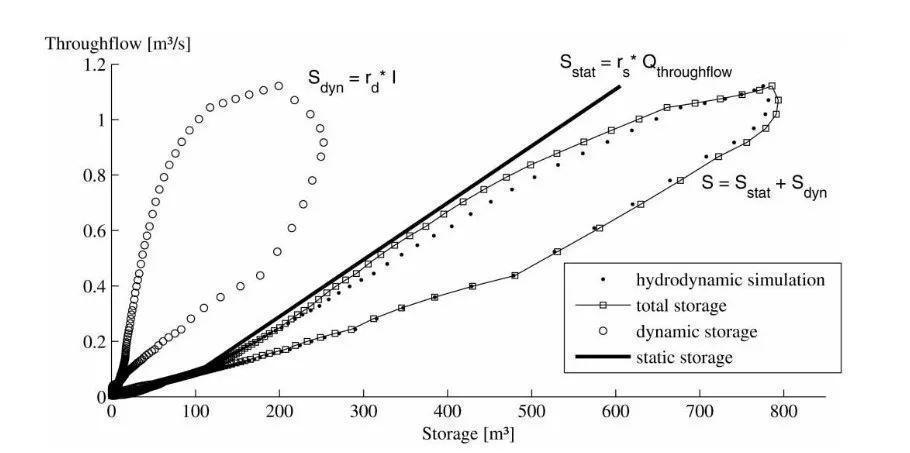
图1 出流和蓄水量间的关系
综上,水箱的蓄水量和其入流、出流、溢流均有关系。为实现半自动识别模型结构和率定,文章采用传递函数(Transfer Function, TF)模型。TF模型中蓄水量方程可表示为入流、出流及其若干阶导数的线性组合。并假设t时刻的出流可以表示为之前若干时刻出流和入流的线性组合,它具有灵活的结构。文章比较了两种概念模型(Conceptual Modelling CM):CM1利用TF模型刻画出流和入流间的关系,并假设SS与出流正比,DS与入流正比;CM2为多个水箱串联,出入流间的关系同样用TS模型刻画。两种概念模型的示意如图2。

图2 两种概念模型的对比
在MATLAB/Simulink中实现了这两种模型,并开发了工具箱。该工具箱根据R2和Young 信息准则(YIC)来判断各种模型结构的拟合程度,避免模型发生过拟合;还可基于最大似然和最小二乘法实现参数自主率定。
在案例研究中,利用Infoworks机理模型生成的数据率定CM1和CM2。率定好的简化模型在出流上都能较好地拟合原模型(如图3)。但CM1峰值下降更快,且收敛更慢,拟合效果不如CM2。对于溢流的模拟,具有更复杂结构的CM2能较好地近似其过程,纳什系数在不同事件下均大于0.75(如图4)。

图3 简化模型出流拟合效果

图4 简化模型溢流拟合效果
使用CM2连续模拟近2个月,速度是机理模型的1000倍以上,并且形状和峰值均能准确模拟(如图5)。

图5 简化模型连续模拟效果
编者点评
本文利用传递函数模型统一表达不同简化模型的模型结构,根据R方和最大似然等判据实现了对简化模型结构和模型参数的自主确定。简化模型运算速度提升效果明显,且对机理模型也有良好的近似效果,可以满足实时控制、不确定性分析等不同用途的需求。这一模型简化和结构选择方式值得参考。
内容源于网络,如有侵权,请联系删除
相关资料推荐:
真空排水系统的原理、方法及应用
https://ziliao.co188.com/p62295169.html
知识点:排水系统简化模型结构的选择方法

