第六章：钢筋混凝土受压构件承载力计算

6.2偏心受压构件正截面承载力计算

钢筋混凝土偏心受压构件多采用矩形截面，截面尺寸较大的预制柱可采用工字形截面和箱形截面。圆形截面主要用于桥墩、桩和公共建筑中的柱。

大量试验表明：构件截面变形符合平截面假定，偏压构件的最终破坏是由于混凝土压碎而造成的。

偏心受压构件的破坏形态与偏心距e0和纵向钢筋配筋率有关。

偏心受压短柱试件的破坏可分为两类：

1、受拉破坏（也称为大偏心受压破坏）

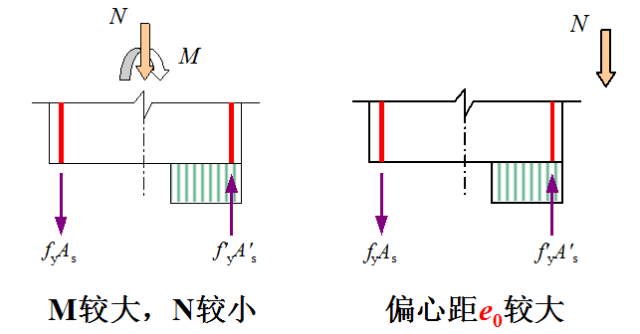
◆轴向压力偏心距较大，截面部分受拉、部分受压。如受拉区配筋量适中，则构件在受力后，受拉区先出现横向裂缝。随着荷载增加，裂缝不断开展延伸，受拉钢筋应力首先达到屈服强度。

◆ 此后，裂缝迅速开展，受压区高度减小。

◆ 最后受压侧钢筋A's 受压屈服，压区混凝土压碎而达到破坏。

◆ 这种破坏具有明显预兆，变形能力较大，破坏特征与配有受压钢筋的适筋梁相似，承载力主要取决于受拉侧钢筋。

◆ 形成这种破坏的条件是：偏心距e0较大，且受拉侧纵向钢筋配筋率合适，通常称为大偏心受压。

2、受压破坏（小偏心受压）

产生受压破坏的条件有两种情况：

⑴当相对偏心距e0/h0较小，截面全部受压或大部分受压。

⑵或虽然相对偏心距e0/h0较大，但受拉侧纵向钢筋配置较多时。

◆ 截面受压侧混凝土和钢筋的受力较大。

◆ 而受拉侧钢筋应力较小。

◆ 当相对偏心距e0/h0很小时，‘受拉侧’还可能出现“反向破坏”情况。

◆ 截面最后是由于受压区混凝土首先压碎而达到破坏。

◆ 承载力主要取决于压区混凝土和受压侧钢筋，破坏时受压区高度较大，远侧钢筋可能受拉也可能受压，破坏具有脆性性质。

◆ 第二种情况在设计应予避免，因此受压破坏一般为偏心距较小的情况，故常称为小偏心受压。

3、受拉破坏和受压破坏的界限

◆ 即受拉钢筋屈服与受压区混凝土边缘极限压应变ecu同时达到。

◆ 与适筋梁和超筋梁的界限情况类似。

◆ 因此，其相对界限受压区高度仍为:

大小偏心受压的分界：

附加偏心距和偏心距增大系数

1、附加偏心距

由于施工误差、荷载作用位置的不确定性及材料的不均匀等原因，实际工程中不存在理想的轴心受压构件。为考虑这些因素的不利影响，引入附加偏心距ea，即在正截面受压承载力计算中，偏心距取计算偏心距e0=M/N与附加偏心距ea之和，称为初始偏心距ei。

参考以往工程经验和国外规范，附加偏心距ea取20mm与h/30 两者中的较大值，此处h是指偏心方向的截面尺寸。

偏心距增大系数η

矩形截面正截面承载力设计计算

非对称配筋截面：构建截面两侧所配置的钢筋不相等（数量或直径不同）。不对称配筋比较经济，但是施工不够方便。

对称配筋截面：构件截面两侧配置了相等的钢筋。对称配筋要多用一些钢筋，但构造简单、施工方便，特别是构件在不同的荷载组合下，同一截面可能承受数量相近的正负弯矩时，更应该采用对称配筋。

一、不对称配筋截面设计

基本公式

1、大偏心受压（受拉破坏）

已知：截面尺寸(b×h)、材料强度( fc、fy，fy' )、构件长细比(l0/h)以及轴力N和弯矩M设计值

若ηei>eib.min=0.3h0，

一般可先按大偏心受压情况计算

1）As和A's均未知时

★若A's<0.002bh

则取A's=0.002bh，然后按A's为已知情况计算。

★若As<ρminbh ，应取As=ρminbh。

2）A's为已知时

先由第二式求解x

★若As<ρminbh ，应取As=ρminbh。

★若As<ρminbh ，应取As=ρminbh。

2、小偏心受压（受压破坏）

另一方面，当偏心距很小时，如附加偏心距ea与荷载偏心距e0方向相反，

则可能发生As一侧混凝土首先达到受压破坏的情况，这种情况称为“反向破坏”。此时通常为全截面受压，由图示截面应力分布，对A's取矩，可得，

e'=0.5h-a'-(e0-ea), h'0=h-a'

重新求解 和A's

用基本公式求解非常麻烦，迭代计算方法

对于Ⅱ级钢筋和

二、不对称配筋截面复核

二、对称截面

相关资料推荐：

第三章 受压构件正截面承载力计算

https://ziliao.co188.com/p62451333.html

知识点：偏心受压构件正截面承载力计算