摘要

悬索桥自重下最终缆形的确定，使其能够安全施工和运行。现有的研究大多是在拉格朗日坐标系下逐段求解主缆的形状。本文利用欧拉描述的非线性有限元方法提出了一种新的悬索桥主缆找形方法。首先建立三维空间主缆的控制微分方程，然后引入一维线形函数，利用牛顿迭代法求解主缆的形状。该方法可方便地简化为求解二维平行缆的形状，该方法需要两个迭代层。使用本方法进行找形的过程中不需要主缆的材料或横截面信息。通过三个案例研究，将常用的分段悬链线方法与现有方法进行比较，即1666米主跨具有二维平行和三维空间缆的地锚悬索桥以及300米主跨具有三维空间缆的自锚式悬索桥，数值研究和迭代结果表明，所提出的找形方法具有足够的精度，且操作方便，可实现主缆的目标线形。

关键词

悬索桥；主缆；找形；非线性有限元法；欧拉描述

1、引言

基础理论、施工技术和新材料的进步，使桥梁跨度快速增大，能够跨越大河、宽峡谷、深海峡。悬索桥作为跨度最大的桥型，从力学性能和经济性能的角度来看，悬索桥始终是单跨超过一公里的首选桥型。虽然最长的悬索桥仍然是1998年建成的主跨1991米的明石海峡大桥，但最近正在建设几座主跨超过2千米的超长悬索桥，例如主跨跨度2023米的土耳其恰纳卡莱1915大桥、位于中国主跨2018米狮子洋大桥和过长江2300米主跨的张高大桥。由于自重或初始拉应力，主缆的重力刚度是悬索桥主跨持续增长的最重要原因之一，其在悬索桥系统刚度中的比例也将随着主跨长度的增加而增加。

本质上，重力刚度源于几何非线性，这在很大程度上取决于主缆的构造和内力。然而，主缆的形状应考虑到所有外力的影响，这在施工过程中总是无法修改。在初步设计阶段，应预先确定由于桥梁自重引起的恒载下主缆在初始平衡状态下的构造或目标形状。因此，进行形状确定或找形过程中，以通过最小化桥梁恒载引起的变形来确定主缆的形状和内力。此外，主缆尺寸的增加和缆索设计安全系数的降低，要求对结构部件中的缆索构造和内力进行更精细的估计。

在过去的几十年里，悬索桥主缆的找形理论受到了广泛的关注。对于给定无应力长度、截面面积、杨氏弹性模量和密度的索段，节点力与节点位移/位置之间存在多种关系，如考虑垂度效应的杆件单元、两节点曲线索单元以及各种二维和三维悬链线索单元。分段抛物线理论假设主缆在均布荷载下的形状为抛物线。这种近似忽略了从吊索传递的集中力，这仅适用于中小跨度悬索桥。

分段悬链线理论允许获得每个索段形状的解析解。在许多开创性的研究中可以找到描述索段在自重作用下的轴向力与应力/无应力长度之间的解析关系的方程。这些方程后来被广泛应用于悬索桥主缆的各种找形方法，如初始力法或分段悬链线法(SCM)，恒载目标构形法（TCUD）、改进的TCUD法、广义TCUD法、坐标迭代法、摄动法等。这些方法中每个主缆段的无应力长度是未知的，并使用非线性有限元迭代在连续非线性方程中求解。通常，在确定主缆的形状之前，至少需要两个循环来计算每个悬链线段的无应力长度和轴向力。为了避免在每个单元上出现循环，在TCUD方法和广义TCUD方法中，在制定切向刚度矩阵时，将每根主缆的无应力长度视为未知参数。基于每个悬链线单元解析解的找形过程基本上是精确的。但其理论推导复杂，算法的实现需要较高的编程能力。此外，它们中的大多数仅限于二维平行主缆。

旨在提高悬索桥横向刚度的三维空间主缆在最近的一些项目中得到应用，如韩国的永宗大桥、中国的江东大桥、美国的新奥克兰湾大桥和挪威的哈洛格兰大桥。唐等人通过迭代主缆的轴向分量，将二维分段悬链线方法扩展到三维，以实现目标垂跨比。Kim等人通过引入三维弹性悬链线索单元，使用改进的TCUD法和初始力法估算了永宗大桥的空间索形状。与平面缆索系统相比，这些研究中的程序对于空间弯曲主缆来说更长、更耗时。

为简化计算过程并减轻计算负担，采用有限元法（FEM）估计三维缆索形状。肖和宋等人提出了五步算法，使用通用有限元软件ANSYS求解二维平面和三维空间缆索形状，在初步设计阶段便于执行。然而，使用通用的有限元程序导致对核心算法的理论分析不够充分。

可以看出，上述大多数方法是在拉格朗日坐标系中提出的，该坐标系将有关的量表示为主缆段未变形位置或无应力长度的函数。然而，每个主缆段的无应力长度通常是未知的，从而导致更多的循环层。本文提出了一种使用非线性有限元和欧拉描述的主缆找形确定程序。通过引入一个条件函数来表示来自吊索的集中力，提出了基于力平衡的整条主缆而不是缆段的修正控制方程。主缆的所有数量均在固定坐标系中表示。即如果将悬索桥沿桥轴线的纵向、竖向和横向定义为x、y和z轴，则与主缆的y坐标和z坐标相关的主缆变量由固定的x坐标表示，而不是由主缆的无应力长度表示。然后从线性基本函数开始进行有限元离散化过程，求解控制偏微分方程，得到一组非线性代数方程。提出了求解已知和未知水平轴向力的缆形的迭代方案。将常用的分段悬链线法与现有方法进行了比较。分别采用本方法和分段悬链线法求解应用1666米主跨地锚式悬索桥的二维平行和三维空间主缆形状。kim等人分析的自锚式永宗大桥也使用所提出的方法进行了检验，以验证其准确性。所提出的算法提供了一种在初步设计阶段仅使用两层迭代和较少编程来估计主缆形状的替代方法。有限元法的使用使得本方法可以很容易地嵌入到一些常用的有限元分析软件中，并且很容易被一般桥梁工程师使用。

2、基于欧拉描述的主缆找形

2.1 空间缆的控制方程

空间主缆在欧拉坐标系中布置如图1所示。沿桥轴的纵向是x轴，垂直方向是y轴，横向为z轴。主缆两端的拉力分解为三个分量，即（H₀、F_y1、F_z1）和（H₀、F_y2、F_z2），主缆的单位重量定义为q，主缆在x方向的投影长度为 L，吊索的总数为n。如图1b所示，第i（i=1，2，…，n）个倾斜吊索的张力表示为T_i，由y方向的垂直力T_yi和z方向的横向力T_zi组成。第i个吊架与主缆的连接位置在(x_i,y_i,z_i)或(x_i,y_i,-z_i)坐标，桥面的另一个连接位置定义为(x_i,y_di,z_di)或(x_i,y_di,-z_di)。

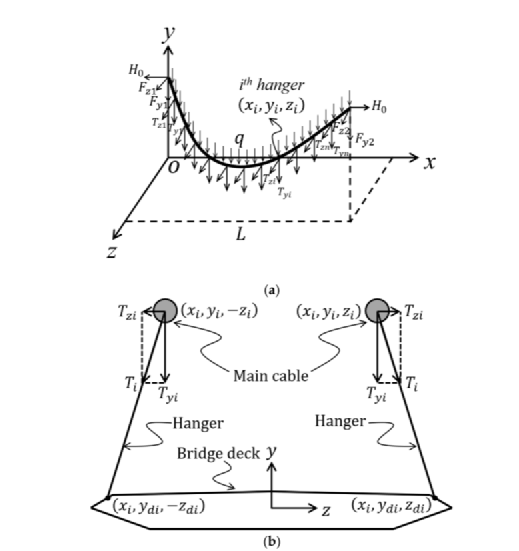
图1空间主缆的坐标系和荷载分布

（a）三维坐标（b）截面的二维坐标

在桥梁的成桥状态，从每个倾斜吊索传递的集中力可以由梁的恒载和吊索的自重确定。还规定了由于主缆重力引起的均布力。为了建立空间缆的平衡方程，本研究采用了四个假设：

（1）悬索桥的主缆是理想的柔性，不承受任何弯矩，只考虑轴向拉力。

（2）主缆的轴向变形很小，使得主缆的横截面面积保持不变，并且单位长度的缆重也是不变的。

（3）所有材料均采用线弹性假设。

（4）主缆上的所有载荷都平行于y-o-z平面。主缆x方向的拉力为常数，定义为H₀。

在初步设计阶段的成型过程中，通常采用前三种假设。张等人的研究表明，主缆的抗弯刚度很小，在施工过程中可以忽略不计。此外，主缆应在屈服应力以下工作，因此轴向变形很小，横截面积的变化可以忽略。对于大多数现代悬索桥，吊索设计成只在桥的横截面上倾斜。每个吊索在纵向上没有或无明显的张力分量。因此，主缆在x方向上的张力保持恒定。沿主缆轴线的拉力假定为F，可分别分解为x、y、z方向的H₀、F_y和F_z。F的方向平行于有关位置的索单元，即d_s=(d_x,d_y,d_z)。F_y,F_z,H₀之间的比率可以表示为：

对方程（1）和 （2）关于x求导的形式为：

F_y和F_z沿x方向的分布也可以表示为实际载荷的函数：

其中δ(x-x_i)是一个条件函数，定义为：

值得注意的是，为了简化公式，本研究此后采用爱因斯坦求和约定，例如等式（5）和（6）中的T_yiδ（x-）=Σⁿ_i=1T_yiδ（x-)。空间缆的控制方程可以通过将方程（3）和（6）组合为：

其中破折号表示相对于x的空间微分。对于平行于x-o-y平面的二维主缆，分配了一个恒定的z坐标。等式(9)和(10)可以简化为：

2.2 缆形的非线性有限元解

定义了一个微分形式的方程f(x,u,u’,u”，…)=0，其中f是函数符号，x是自变量，u是因变量，u’,u”，…是关于x的一阶、二阶和高阶导数。在有限元中，可以使用基函数或形状函数对其进行离散化，得到∫_Ω f(x,u,u’,u”，…)N_idΩ = 0的次形式，其中Ω是有关的计算域。为了求解缆形，本研究采用一维线性函数，形式为：

其中，a_i1和a_i2是由元素节点坐标估计的待定系数。利用伽辽金方法，主缆形状用Y(x)和Z(x)可表述为：

通过引入N_i（x），方程（9）和（10）的离散代数形式或次形式可以表示为：

其中下标j（j=1,2,…, n)表示吊索编码，在应用爱因斯坦求和约定之前引入它是为了与下标i进行区分。以下部分中的下标k和l也用于相同目的。部分积分应用于方程（15）和（16），这得到：

其中BC表示积分边界条件。将等式（8）代入等式（17）和（18）得出：

其中y_i和z_i是主缆最终y方向和z方向的坐标。关于T_yi和T_zi之间比率的附加公式如下：

如等式（12）所示，一维线性函数相对于x的微分是元素的常数。同时，假设主缆位于索塔顶部的节点是固定的。因此狄利克雷边界条件应用于y和z的变量。等式（19）和（20）的积分形式可以使用如下形式的求和来交替求解：

其中dL是元素Ω_e在x方向上的长度。值得注意的是在每个元素内都是常数，但是对于不同的元素，它们的值并不相同。为了求解这个与y_i和z_i有关的非线性方程，引入了牛顿迭代法:

其中f(x)是要求解的函数，x_n+1是f(x)=0在(n+1)步迭代时的近似解,ω是松弛系数,在本研究中设置为1。等式（22）和（23）中的f’(x_n)是多变量问题的矩阵，由目标函数对每个未知变量的偏导数组成：

其中f_yi和f_zi是方程(22)和(23)的第一个部分描述的函数，它们分别从y方向方程（9）和z方向方程（10）在第i点处的平衡方程导出，用于选择的一维线性函数。为了构造主缆的牛顿迭代形式方程（22）和（23），与f’(x_n)相关的矩阵和与f(x_n)相关的向量组合为：

其中k^yy、k^yz、k^zy、k^zz、f_y和f_z是通过将所有元素的k^yy_ij、k^yz_ij、k^yz_ij、k^zz_ij,f_yi和f_zi组合得到的，k_yy、k_yz、k_zy和k_zz是n×n矩阵,和是n×1的矩阵。为了求解主缆在y和z方向的变形增量，即Δ=(dy dz)^T，然后建立线性代数方程，其形式为:

使用(y_i z_i)和(dy_i dz_i)的总和很容易更新主缆的节点坐标。值得注意的是，迭代前的初始节点坐标(y_i z_i)可以指定为任意值，为了方便建议使用索塔与主缆交点（IP）的坐标。上述迭代方案如图2所示，给定H₀，在本研究中称为内层迭代。

图2求解缆形的迭代方案流程图

然而，在大多数情况下，H₀是一个未知的参数。主缆在y方向上的中点坐标y_mid或跨中垂度f总是预先确定的。因此，实现了外层迭代，如图2所示。在每次外层迭代中，y方向中点的坐标_mid可以通过给定的H₀使用内层迭代求解。假设一对一的映射关系_mid=g()，其中g()是函数符号。因此，H₀的解可以通过找到方程G（H₀）=g(H₀)-y_mid=0的根来确定。由于g(H₀)没有明确的表达式，因此利用割线法来获得H₀的数值解。H₁和H₂的初始条件建议为1.0倍和 1.1倍。

对于二维平行主缆，主缆在z方向上的坐标是一个不变的常数。由于K=k_yy,可简化为一个n×n的矩阵，其中k_yy是从k^yy_ij通过去除等式(25)中与Z_i相关的项组装而成的,其形式为:

2.3 对比分段悬链线法

分段悬链线法是主缆单元因自重而变形的精确解。x、y和z方向上每段的长度求解为：

其中lx、ly和lz是沿全局坐标x、y和 z轴的线段的两个节点之间的距离，Fx、Fy和Fz是全局节点力的三个分量,Ec是主缆的弹性模量，Ac为横截面积，q为单位长度主缆自重，l₀为主缆段的无应变长度。分段悬链线法的迭代方案如图3所示。对于双塔悬索桥，先猜测主索一端的轴向力F₁=(F_x1,F_y1 ,F_z1)。通过求解方程（34）和（36）中描述的方程得到第一段的无应变长度l₀₁和l_y1和l_z1。下一段的轴向力将用于求解l₀₂和l_y2和l_z2,然后通过引入第一个吊索的张力很容易计算。将通过比较y方向和z方向上另一个索塔的IP坐标，即y_ip和z_ip与计算的_IP和_IP以及y_mid和_mid来调整F₁以实现收敛解。

图3 分段悬链线法求解缆形的迭代方案流程图

分段悬链线法与现有的非线性有限元法的比较如表1所示。分段悬链线的重点在每个主缆段上，以使用拉格朗日坐标系中的代数方程（方程（34）和（36））建立其关于主缆无应力长度l₀的缆形解析表达式。本文采用非线性有限元近似方法，在欧拉坐标系下，以桥轴为坐标，求解全缆的微分方程组。分段悬链线需要输入主缆的轴向刚度，即EcAc来确定主缆的无应力长度，而非线性有限元不需要关于主缆材料或截面的信息便可求解主缆的形状。值得注意的是，在施工阶段非常重要的索无应力长度也可以用非线性有限元法通过主缆的最终长度中减去伸长量来计算。

表1 分段悬链线与非线性有限元比较

3、案例研究

3.1 案例一：二维平行缆的地锚式悬索桥

研究带有二维平行缆的地锚式悬索桥，如图4所示。主跨1666m且下垂172.64m，边跨500m，设计垂跨比为9.65，采用宽度为49.7m的单箱梁。桥塔高度为265m，塔架顶部两个IP点的高程为267.414m。有两个平行的竖直索面，每个索面由一根主缆和边跨29根吊索和主跨103根吊索组成。z方向两根平行主缆的间距为41m。x方向边跨主缆段的长度为35m+28×16m+17m,中跨长度为17m+102×16m+17m。主缆单位长度自重q为54.088KN/m。主缆的弹性模量为1.96E11N/m，横截面面积Ac为0.706。欧拉坐标系的原点设置在桥的中点，高程为零。

图4平行缆悬索桥布置图

通过引入梁的边界条件，从加劲梁的恒载估计每个吊索T_yi在y方向上的节点力或拉力。梁和索塔之间的交点在y方向上的位移是耦合的。主梁和过渡墩之间的交点在y和z方向以及相对于x轴的旋转自由度上耦合。y方向上估算的索力如图5所示。最大值3781.2kN出现在边跨第一个吊索处，而大多数吊索的拉力为2372.52kN。初始垂度f=172.64m，表明y_mid=267.414-172.640=94.774m。

图5沿桥跨Y方向吊索力

按照图2中的方案，使用两层迭代来进行主缆的找形。外层和内层迭代公差设置为ε1=1.0×和ε2=1.0×。图6给出了迭代结果，其中轴向力的水平分量H₀在五个外层迭代步骤中得到收敛。在每个相邻的外层迭代之间，求解主缆形状所需的内层迭代少于四步。从初始输入坐标到与最终外层和内层迭代出相对应的最终找形结果的主缆形状如图7所示。并以常用的分段悬链线法(SCM)为基准进行了找形比较。图8a中给出了本研究和SCM得出的最终主缆形状，显示了彼此之间的一致性。各吊索节点的最大相对差值为0.0011%。并将按y=y_ip+4f(x²-L²/4)/L²计算的中跨主缆线形与现有解作了比较，如图8b所示。两种方法的差异很小，最大相对误差为0.0948%。这主要是因为该悬索桥的垂跨比约为1/10，使得沿桥的静荷载大致服从均匀分布。此外，利用有限元法分析了最终主索在自重和吊索拉力作用下的静位移，如图9所示。可以看出，主缆所有节点位移均小于0.007m，它足够小，可以使主缆达到目标构型。值得注意的是，在这种情况下非线性有限元法和分段悬链线法所用时间都不到一秒钟。

图6二维平行缆内外层迭代结果

图7二维平行主缆从初始坐标到目标布置的缆形

图8平行主缆缆形对照

（a）非线性有限元与分段悬链线对比

（b）非线形有限元与抛物线理论对比

图9有限元法得到的二维平行主缆的静位移

3.2 案例二：三维空间缆的地锚式悬索桥

三维空间主缆应用于与案例一相同的悬索桥。两根主缆点和IP点在z方向上的的间距分别设置为63.0m和3.0m，如图10所示。图5给出了与案例一相同的吊索竖向分力。本案例中应用相同的公差，ε1 =1.0×和ε2=1.0×，迭代过程如图11所示。与案例1相同，进行了五次外层迭代便获得了收敛的H₀。所有内层迭代都少于五步，便满足公差要求。主缆形状从y和z方向的初始输入坐标到最终目标构形如图12所示。案例1中 二维平行主缆的最终形状也绘制在图12a中。可以看出，二维平面缆和三维空间缆在y方向的形状非常匹配。这可以通过比较方程（9）和（11）描述的缆形控制方程来解释。平行和空间情况下x-o-y平面中缆形的差异主要归因于 z'。对于本案例研究的大跨度悬索桥，空间索z方向坡度比y方向坡度小，导致方程(9)和(10)中Z^’2的影响不明显。这也可以从图12中的最终缆形中得到证明。使用中心差分法计算得到的最大值Y^’2和Z^’2分别为0.2593和0.0033。

图10 空间缆悬索桥俯视图（一半桥）

图11 案例二空间缆地锚式悬索桥内外层迭代结果

图13 三维空间缆从初始坐标到目标构形的主缆形状

(a)y方向 （b）z方向

图片13说明了沿桥跨z方向吊索拉力分量的解。正拉力表示吊索的倾角向内倾斜。z方向最大正拉力出现在跨中，值为331.637kN。两边跨向外倾斜的第一或末尾吊索负拉力达到最大值。这是因为如图 5所示的第一个或末端吊索索力的垂直分量很大。图14比较了本研究与分段悬链线获得的最终缆形。在y和 z方向上所有吊索节点的最大相对差值分别为0.0022%和0.7318%，表明彼此之间存在一致性。为进一步验证最终缆形的准确性，还建立了空间主缆的有限元模型。自重和吊索力作用下的静位移如图15所示。可以发现，主缆在y方向和z方向的最大位移分别为0.008m和0.012m，对于工程应用来说已经足够小并且可以接受。

图13 沿桥跨z方向的吊索力分量

图14 非线性有限元与分段悬链线得到三维主缆缆形状比较

（a）y方向 （b）z方向

图15 有限元得到三维空间缆位移

（a）y方向 （b）z方向

3.3 案例三：三维空间缆的自锚式悬索桥

另一个例子是韩国的永宗大桥，对其找形进行了许多开创性研究。永宗大桥是第一座采用三维主缆的公铁两用自锚式悬索桥，总长550m,300m主跨和两个125m的边跨，中跨垂度为60m。T_yi为3.048 KN的统一值，主缆横截面积为0.1355。通过将欧拉坐标系原点设置在桥梁零高程的中点，IP点的y和z坐标值分别为y_ip=114.573m和z_ip=1.50m。主缆通过23根吊索分成24段。根据kim等人和罗等人给出的数据估计吊索和梁之间连接点的坐标，即y_di和z_di，如表2所示。IP点位于x=125.0m，主跨中点位于x=275.0m处。

   表2 吊索与主梁连接点坐标值

永宗大桥使用本方法迭代过程如图16所示。外层和内层迭代五步均满足容差要求。求解的主缆轴向力水平分量为48149.1kN，与kim等人给出的值49541kN 接近，有2.89%相对误差。缆形的解与kim等人和罗等人获得的结果在表3中进行了比较。可以看出，本研究与kim等人在y方向上的相对差异小于 0.027%，在z方向，相对差的绝对值小于0.340%。罗等人进一步研究了IP点的位置，这与本研究和kim等人使用的坐标不同。本研究与罗等人的差异的最大绝对值在y和 z方向上分别为0.041%和0.524%，略大于本研究与kim等人研究之间的误差。本方法被证明足够准确，可以为工程应用找到合理的悬索桥缆形。

图16 案例三三维空间缆内外层迭代结果

   表3 本研究结果与其他研究结果的比较

4、结论

本文提出了一种新的找形方法，适用指定荷载下的主缆系统。构造了欧拉坐标系下主缆的控制微分方程。然后，使用非线性有限元进行两层数值迭代以求解控制方程。将所提出的方法应用于地锚式悬索桥的二维平行和三维空间主缆以及自锚式悬索桥空间主缆三种情况，达到主缆的目标构形。还与分段悬链线和其他研究进行了比较，以验证本方法的准确性。一些结论可以总结如下：

（1）所提出的找形方法能够有效和准确地估计悬索桥主缆的目标线形。

（2）与常用的分段悬链线相比，提出的非线性有限元使用几个迭代步骤在欧拉坐标系中对整个主缆进行找形，无需任何主缆材料或横截面积信息。主缆无应力长度也可以通过主缆的最终长度减去伸长量来计算。

（3）分段悬链线和提出的非线性有限元方法都具有足够的效率和准确性来找到悬索桥的最终缆形。所提出的技术为工程师在初步设计阶段快速估计二维平行和三维空间缆形提供了一种替代方案。

相关资料推荐：

[广东]独塔悬索桥非对称空间自锚式缆索系统设计图纸56张（两根主缆每根主缆33股）

https://ziliao.co188.com/d62752832.html

知识点：一种基于非线形有限元法的悬索桥主缆找形新方法